Credibility alert: the following post contains assertions and speculations by yours truly that are subject to, er, different interpretations by those who actually know what the hell they’re talking about when it comes to statistics. With hat in hand, I thank reader BKsea for calling attention to some of them. I have changed some of the wording—competently, I hope—so as not to poison the minds of less wary readers, but my original faux pas are immortalized in BKsea’s comment.
Lies, Damned Lies, and…
A few days ago my colleague, Dr. Harriet Hall, posted an article about acupuncture treatment for chronic prostatitis/chronic pelvic pain syndrome. She discussed a study that had been performed in Malaysia and reported in the American Journal of Medicine. According to the investigators,
After 10 weeks of treatment, acupuncture proved almost twice as likely as sham treatment to improve CP/CPPS symptoms. Participants receiving acupuncture were 2.4-fold more likely to experience long-term benefit than were participants receiving sham acupuncture.
The primary endpoint was to be “a 6-point decrease in NIH-CSPI total score from baseline to week 10.” At week 10, 32 of 44 subjects (73%) in the acupuncture group had experienced such a decrease, compared to 21 of 45 subjects (47%) in the sham acupuncture group. Although the authors didn’t report these statistics per se, a simple “two-proportion Z-test” (Minitab) yields the following:
Sample X N Sample p
1 32 44 0.727273
2 21 45 0.466667
Difference = p (1) – p (2)
Estimate for difference: 0.260606
95% CI for difference: (0.0642303, 0.456982)
Test for difference = 0 (vs not = 0): Z = 2.60 P-Value = 0.009
Fisher’s exact test: P-Value = 0.017
…
Wow! A P-value of 0.009! That’s some serious statistical significance. Even Fisher’s more conservative “exact test” is substantially less than the 0.05 that we’ve come to associate with “rejecting the null hypothesis,” which in this case is that there was no difference in the proportion of subjects who had experienced a 6-point decrease in NIH-CSPI scores at 10 weeks. Surely there is a big difference between getting “real” acupuncture and getting sham acupuncture if you’ve got chronic prostatitis/chronic pelvic pain syndrome, and this study proves it!
Well, maybe there is a big difference and maybe there isn’t, but this study definitely does not prove that there is. Almost two years ago I posted a series about Bayesian inference. The first post discussed two articles by Steven Goodman of Johns Hopkins:
I won’t repeat everything from that post; rather, I’ll try to amplify the central problem of “frequentist statistics” (the kind that we’re all used to), and of the P-value in particular. Goodman explained that it is logically impossible for frequentist tools to “both control long-term error rates and judge whether conclusions from individual experiments
[are] true.” In the first article he quoted Neyman and Pearson, the creators of the hypothesis test:
…no test based upon a theory of probability can by itself provide any valuable evidence of the truth or falsehood of a hypothesis.
But we may look at the purpose of tests from another viewpoint. Without hoping to know whether each separate hypothesis is true or false, we may search for rules to govern our behaviour with regard to them, in following which we insure that, in the long run of experience, we shall not often be wrong.
Goodman continued:
It is hard to overstate the importance of this passage. In it, Neyman and Pearson outline the price that must be paid to enjoy the purported benefits of objectivity: We must abandon our ability to measure evidence, or judge truth, in an individual experiment. In practice, this meant reporting only whether or not the results were statistically significant and acting in accordance with that verdict.
…the question is whether we can use a single number, a probability, to represent both the strength of the evidence against the null hypothesis and the frequency of false-positive error under the null hypothesis. If so, then Neyman and Pearson must have erred when they said that we could not both control long-term error rates and judge whether conclusions from individual experiments were true. But they were not wrong; it is not logically possible.
The idea that the P value can play both of these roles is based on a fallacy: that an event can be viewed simultaneously both from a long-run and a short-run perspective. In the long-run perspective, which is error-based and deductive, we group the observed result together with other outcomes that might have occurred in hypothetical repetitions of the experiment. In the “short run” perspective, which is evidential and inductive, we try to evaluate the meaning of the observed result from a single experiment. If we could combine these perspectives, it would mean that inductive ends (drawing scientific conclusions) could be served with purely deductive methods (objective probability calculations).
These views are not reconcilable because a given result (the short run) can legitimately be included in many different long runs…
It is hard to overstate the importance of that passage. When applied to the acupuncture study under consideration, what it means is that the observed difference between the two proportions, 26%, is only one among many “outcomes that might have occurred in hypothetical repetitions of the experiment.” Look at the Minitab line above that reads “95% CI for difference: (0.0642303, 0.456982).” CI stands for Confidence Interval: in the words of BKsea, “in 95% of repetitions, the 95% CI (which would be different each time) would contain the true value.” We don’t know where, in the 95% CI generated by this trial (between 6.4% and 45.7%), the true difference lies; we don’t even know that the true difference lies within that interval at all (if we did, it would be a 100% Confidence Interval)! Put a different way, there is little reason to believe that the “center” of the Confidence Interval generated by this study, 26%, is the true proportion difference. 26% is merely a result that “can legitimately be included in many different long runs…”
Hence, the P-value fallacy. It is that point—26%—that is used to calculate the P-value, with no basis other than its being as good an estimate, in a sense, as any: it was observed here, so it can’t be impossible; when looked at from the point of view of whatever the true proportion difference is, it has a 95% chance of being within two standard deviations of that value, as do all other possible outcomes (which is why we can say with ‘95% confidence’ that the true proportion is within two standard deviations of 26%). You can see that the CI is a better way to report the statistic based on the data, because it doesn’t “privilege” any point within it (even if many people don’t know that), but the CI will also steer us away from being wrong only in “the long run of experience.” CIs, of course, will be different for each observed outcome. The P-value should not be used at all.
Now let’s look at a graph from the acupuncture report:
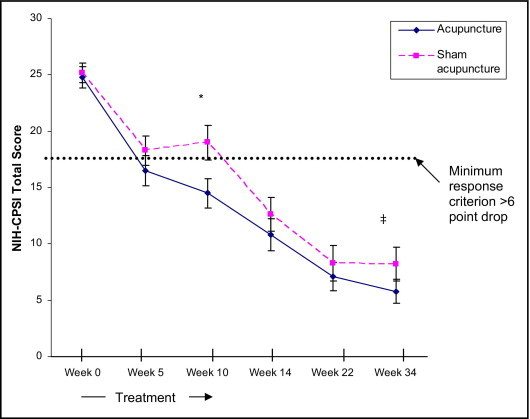
- Figure 3. Mean NIH-CPSI total scores of 89 chronic prostatitis/chronic pelvic pain patients treated with 20 sessions of either acupuncture (n = 44) or sham acupuncture (n = 45) therapy over 10 weeks. Error bars represent the SD. To enter into the study, each participant had a minimum NIH-CPSI total score of at least 15 (range 0-43) on both baseline visits (indicated as the average in the baseline value). The primary criterion for response was at least a 6-point decrease from baseline to week 10 (end of therapy). There was no significant difference between the NIH-CPSI total scores in the acupuncture and sham acupuncture groups at baseline, week 5 (early during therapy), or weeks 14, 22, and 34 (post-therapy) evaluations. *Of 44 participants in the acupuncture group, 32 (72.7%) met the primary response criterion, compared with 21 (46.7%) of 45 participants in the sham acupuncture group (Fisher’s exact test P = .02). ‡At week 34, 14 (31.8%) of 44 acupuncture group participants had long-term responses (with no additional treatment) compared with 6 (13.3%) of 45 sham acupuncture group participants (RR 2.39, 95% CI, 1.0-5.6, Fisher’s exact test P = .04).
Hmmm. I dunno about you, but at first glance what I see are two curves that are pretty similar. They differ “significantly” at only two of the six observation times: week 10 and week 34. Why would there be a difference at 10 weeks (when the treatments ended), no difference at weeks 14 and 22, and then suddenly a difference again? Is it plausible that the delayed reappearance of the difference is a treatment effect? The “error bars” don’t even represent what you’re used to seeing: the 95% CI. Here they represent one standard deviation, not two, and thus only about a 68% CI. Not very convincing, eh?
OK, I’m gonna give this report a little benefit of the doubt. The graph shown here is of mean scores for each group at each time (lower scores are better). That is different from the question of how many subjects benefited in each group, because there could have been a few in the sham group who did especially well and a few in the ‘true’ group who did especially poorly. It is bothersome, though, that this is the only graph in the report, and that the raw data were not reported. Do you find it odd that the number of ‘responders’ in each group diminished over time, even as the mean scores continued to improve?
Just for fun, let’s see what we get if we use the Bayes Factor instead of the P-value as a measure of evidence in this trial. Now we’ll go back to the primary endpoint, not the mean scores. Look at Goodman’s second article:
Minimum Bayes factor = e-Z²/2
At 10 weeks, according to our statistics package, Z = 2.60. Thus the Bayes factor is 0.034, which in Bayes reasoning is “moderate to strong” evidence against the null hypothesis. Not bad, but hardly the “P = 0.009” that we have been raised on and most of us still cling to. The Bayes factor, of course, is used together with the Prior Probability to arrive at a posterior probability. If you look on p. 1008 of Goodman’s second paper, you’ll see that as strong as this evidence appears at first glance, it would take a prior probability estimate of the acupuncture hypothesis being true of close to 50% to result in a posterior probability (of the null being true) of 5%, our good-ol’ P-value benchmark. Some might be willing to give it that much; I’m not.
Now for the hard part
This has been a slog and I’m sure there are only 2-3 people reading at this point. Nevertheless, here’s a plug for previous discussions of topics that came up in the comments following Harriet’s piece about this study:
Science, Reason, Ethics, and Modern Medicine, Part 5: Penultimate Words
Science, Reason, Ethics, and Modern Medicine, Part 4: is “CAM” the only Alternative?
Science, Reason, Ethics, and Modern Medicine, Part 3
Science, Reason, Ethics, and Modern Medicine, Part 2: the Tortured Logic of David Katz
